Non Deterministic F. Automata
Deterministic Finite Automata
Espressione regolare
Grammatica di tipo 2

 
Esercizio
Sia dato l'automa non deterministico
M = {{q₀, q₁}, {0,1}, §, {q₀}, {q₁}}

§(q₀,0) =  {q₀, q₁}
§(q₀,1) = {q₁}
§(q₁,1) = {q₀, q₁}

Determinare il linguaggio accettato dall'automa, definire una grammatica di tipo 3 che lo genera e definire un automa deterministico equivalente.

Soluzione:
Rappresentiamo graficamente l'automa.

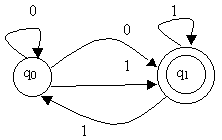
A volte capire il linguaggio generato da un automa non e' semplice, e a mio avviso lo è ancor meno quando l'automa e' di tipo non deterministico (Non Deterministic Finite Automata - NDFA). Quindi conviene trovare un automa deterministico equivalente (Deterministic Finite Automata - DFA).

Ripasso di un argomento di matematica discreta (algebra):
L'insieme delle parti: Se l'insieme A e' costituito dai seguenti elementi: A={1,2,3}
l'insieme delle parti, ossia l'insieme di tutti i possibili sottoinsiemi definibili da questo insieme, è così fatto:
P(A) = { / , {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}. Le parti sono 8, con / = insieme vuoto. In generale il numero di tutte le possibili parti, ossia |P(A)| e' 2 ⁿ se |A| = n.

Per definire un automa deterministico equivalente a partire da uno non deterministico, ricaviamoci prima tutte le possibili parti dall'insieme degli stati del NDFA.
K = insieme degli stati = {q ₀, q₁}
allora P(K)={/, {q₀}, {q₁}, {q₀, q₁}}. Ogni sottoinsieme di A è uno stato del nuovo automa deterministico, insieme vuoto (/) compreso. La funzione di transizione è:

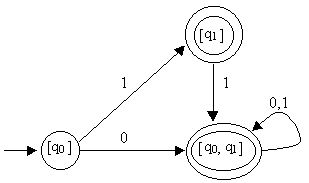
§([q0],0)=[q0, q1] §([q0],1)=[q1] §([q1],0)=/ §([q1],1)=[q0, q1] §([q0, q1],0)=[q0, q1] §([q0, q1],1)=[q0, q1]

 
L'insieme F¹ (l'insieme degli stati finali dell'automa deterministico) e' un sottoinsieme di P(K)  in cui è presente almeno uno stato di accettazione (q ₁).
A questo punto risulta piu' semplice capire il inguaggio accettato. q₀ rimane sempre il nostro stato iniziale. Se scelgo di andare in [q₁] riconosco 1 e posso fermarmi oppure posso proseguire per [q₀q₁] (e quindi ho riconosciuto 11). Arrivato in [q₀q₁] posso fermarmi o riconoscere qualsiasi tipo di stringa di 0 e 1,  (0+1)^*.
Riassumendo,  l'espressione regolare corrispondente al linguaggio accettato dell'automa e': (0+1+11)(0+1)*

Non ci rimane che trovare la grammatica di tipo 3 che lo genera:
 

S->0A | 1B | 0 | 1
A->0A | 1A | 0 | 1
B->1A | 1
 

© C o p y r i g h t     1 9 9 4 - 2 0 0 4 w w w . d i z i o n a r i o i n f o r m a t i c o . c o m