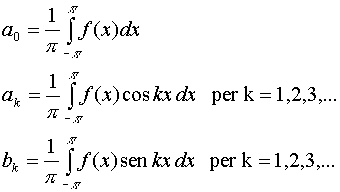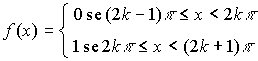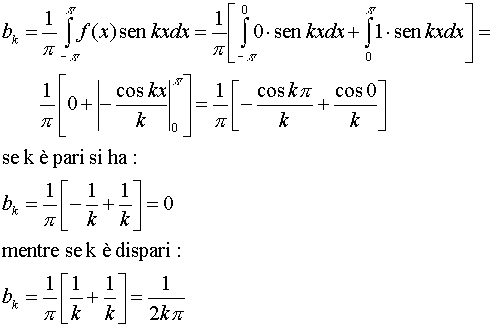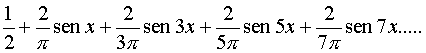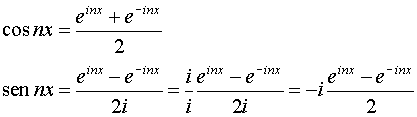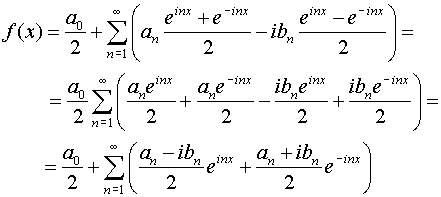La serie di Fourier

 Se f(x) è una funzione periodica di periodo 2, integrabile nell'intervallo (-,) si chiama serie di Fourier ad essa associata la serie trigonometrica

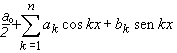
Ecco come ottenere i coefficienti :

Esercizio svolto:

Per fare un esempio svolgiamo quindi un esercizio esplicativo sviluppando in serie di Fourier la funzione così definita:

Se tracciamo il grafico della funzione:

y = 0 k = 0 - x < 0 k = 1 x < 2 k = 2 3 x < 4 k = 3 5 x < 6 .......

y = 1 k = 0 0 x < k = 1 2 x < 3 k = 2 4 x < 5 k = 3 6 x < 7 .......

Nei punti -,0, la funzione presenta punti di discontinuità di prima specie.

Def:Punto di discontinuità: punto p del dominio della funzione f(x) per cui il limite della funzione per x che tende a p non esiste oppure esiste ma non coincide con f(p).

Def. Punto di discontinuità di prima specie: i punti di discontiunità di prima specie sono quei punti per cui il limite destro e sinistro esistono ma differiscono entrambi da f(p).

Sono pertanto soddisfatte le Condizioni di Dirichlet. Troviamo quindi i coefficienti della serie trigonometrica:

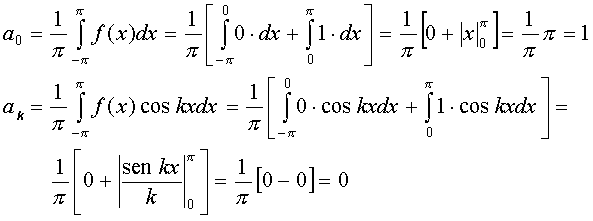
 Quindi trovàti i coefficienti possiamo sostituirli nella Serie di Fourier .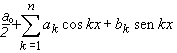

 In forma compatta ;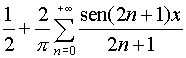

Serie di Fourier in forma complessa:

Data la serie di Fourier per la funzione periodica f(x) di periodo 2:
f(x)=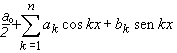 se esprimiamo sen nx e cos nx con le formule di Eulero otteniamo:

sostituendo cos nx e sen nx nella formula otteniamo:

Ora se poniamo:

© C o p y r i g h t     1 9 9 4 - 2 0 0 4 w w w . d i z i o n a r i o i n f o r m a t i c o . c o m