Programmi commentati per la calcolatrice programmabile
HP Serie 48G
« 1 -> Z
«A
1 A SIZE HEAD
FOR Q
Z A SIZE HEAD
FOR P
{Q P} 0 PUT
NEXT
1 'Z' STO+
NEXT
»
» |
L. Data una matrice di dimensioni NxN, costruiamo un programma che azzera gli elementi della diagonale principale, nonche' gli elementi al di sopra della stessa. Z = 1 mette nello stack la matrice A per renderla triang. alta da 1 alla dim. di A da Z alla dim. di A metti a 0 gli elem. di riga P e colonna Q la variabile Z viene incrementata di 1 |
« A -> DIAG
A SIZE
DIAG->
» |
D
nello stack viene messa la matrice A: [[1 2] [3 4]] da cui vengono ottenuti gli elementi diagonali [1 4]. Con A SIZE si ottiene la dim. di A: {2 2} DIAG-> mette nella diagonale di una matrice con le dim. precedenti gli elementi in cima allo stack, ossia [1 4]. Quindi: [[1 0] [0 4]] |
« A SIZE HEAD IDN L D + INV A * - SRAD LOG NEG » |
ES.
La matrice di iterazione di Seidel e' cosi' fatta:
ES = I - (L + D)-1 ·A Si vuole calcolare la velocita' asintotica di convergenza del metodo iterativo di Seidel. Per convenienza il programma oltre a definire ES a partire da A, D, L, includera' anche il calcolo della velocita' asintotica di convergenza (R = -log|λ|) ad una soluzione del sistema lineare Ax = b nei limiti di un'approssimazione. riga 1: definisce una matrice identita' con le stesse dim di A. riga 2,3: calcola la matrice inversa di (L + D) che andra' a moltiplicare A riga 4: il prodotto verra' sottratto alla matrice I(dentita). riga 5: SRAD e' una funzione predefinita che calcola il raggio spettrale della matrice ottenuta in riga 4. Di seguito viene calcolato il logaritmo di segno negato. |
« 1 DIM FOR P ' V¯ Σ (j=1, DIM, A(p,j)^2)' -> NUM NEXT DIM -> LIST «*» STREAM A DET ABS / »ove DIM e' la dimensione della matrice, cosi' definita: « A SIZE HEAD» |
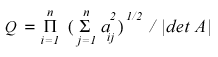Q. Un sistema Ax=b si dice mal condizionato
quando a piccole variazioni dei coefficienti della matrice A o del termine noto b,
corrispondono grandi variazioni nella soluzione x.
Q e' un indice di condizionamento di una matrice. Se Q e' molto grande si dice che la
matrice e' mal condizionata, se invece Q = 1 il sistema non lo e', e siamo nel caso piu'
favorevole per la soluzione (per altri dettagli si rimanda al libro del prof.
Gambolati G., Lezioni di metodi numerici).
A fianco si riporta come viene calcolato Q con la calcolatrice programmabile HP48G(X).
|
| © C o p y r i g h
t 1 9 9 4 - 2 0 0 4 w w w . d i z i o n a r i o i n f o r m a t i c o . c o m |
 |