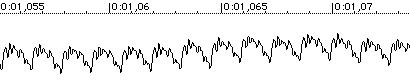Fourier

Ci sono molti fenomeni oscillatori in natura, per esempio, le onde del mare, le maree, le pulsazioni cardiache, la corda vibrante di una chitarra ecc. ed altre meno evidenti quali le molecole d'aria che con la loro oscillazione ci permettono di percepire suoni e rumori.

Non solo i corpi dotati di massa ma anche la luce, le onde radio e in generale le onde elettromagnetiche sono esempi di moti oscillatori.

Tutti questi tipi d'onda non trasportano materia ma energia, basti pensare alle onde marine quando muovono un oggetto galleggiante, questo non si sposta in direzione delle onde ma in direzione perpendicolare a quella delle onde, su e giù, e per tale motivo questo tipo di onde sono definite come onde trasversali. In genere lo studio dei fenomei oscillatori interessano l'acustica, l'elettrotecnica, la meccanica delle vibrazioni, l'astronomia e molte altre scienze.

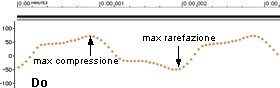
Un segnale sonoro solitamente viene rappresentato con un grafico cartesiano avente in ascissa il tempo e in ordinata i valori istantanei dell'ampiezza che indica un aumento dalla pressione atmosferica (in atm.) o un abbassamento della stessa, in quest'ultimo caso si osserva il fenomeno di rarefazione dell'aria (si ricordi che il suono si propaga anche in mezzi più densi come l'acqua, metalli ecc.).

In acustica si distingue il suono dal rumore per la perturbazione prodotta giacché un suono è prodotto da una vibrazione periodica mentre il rumore no.

Vedremo che questo fenomeno periodico, come quello delle onde elettromagnetiche verrà associarlo ad una funzione periodica.

Iniziamo col riportare i diagrammi delle note musicali prodotte da un flauto, strumento musicale considerato fra i più "puri" poiché la sua rappresentazione grafica mostra la sinuosita' regolare (piu'evidente nel La), al contrario di altri strumenti le cui onde periodiche hanno un andamento molto più complesso (timbro diverso) ma pur sempre periodico.

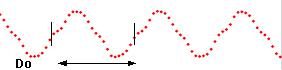
Il Periodo:

Il periodo T è quell'intervallo di tempo tale per cui la vibrazione si ripete con perfetta regolarità, possiamo anche dire che è il tempo necessario all'onda per percorrere la distanza di una lunghezza d'onda.

Diremo che una funzione f(x) di dominio D si dice periodica di periodo T se per qualunque x in D (dominio) e per qualunque k in Z si ha che x+kT appartiene a D e T è il più piccolo reale positivo per cui si verifica l'uguaglianza.Quindi se f(x) ha un andamento sinusoidale questo si ripete al variare di k in Z.

La frequenza:

E' il numero che indica la quantità di oscillazioni complete al secondo compiute da f(x) e si indica con la lettera v (ni), si misura in Hertz (Sistema Internazionale - Hz) per cui un Hz corrispondono ad n oscillazioni al secondo, in formula la frequenza si indica con

Quindi osservando la formula, all'aumentare del periodo T diminuisce la frequenza.

Rifacendoci al fenomeno del suono e in particolar modo alla voce maschile e femminile, ciò che fondamentalmente determina la maggior acutezza della voce, ossia l'altezza del suono, è proprio la frequenza. Infatti la frequenza nella voce maschile varia tra i 100 e 125 Hz mentre per quella femminile tra i 200 e 250 Hz. Diremo quindi che quest'ultima ha un altezza (da non confondere con l'intensità o volume del suono) che è circa il doppio di quella maschile. Similmente analizzando i 7 Do presenti nella tastiera di un pianoforte notiamo che il primo Do, il più grave ha una frequenza di 32 Hz (la corda del pianoforte oscilla 35 volte al sec) che è proprio la metà del Do successivo, e questo è metà del terzo e cosi via...

Do della prima ottava	32 Hz	Do della prima ottava
Do della seconda ottava	64 Hz
Do della terza ottava	128 Hz
Do della quarta ottava	256 Hz
Do della quinta ottava	512 Hz	Do della seconda ottava
Do della sesta ottava	1024 Hz
Do della settima ottava	2048 Hz
Do dell'ultima ottava	4096 Hz

La Pulsazione

Si indica con wè data da:

In un moto circolare uniforme corrisponde alla velocità angolare, come si può notare differisce per il fattore 2 e si misura in rad/sec

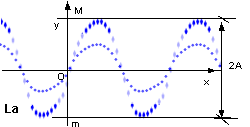
L'Ampiezza

E' il carattere che distingue i suoni forti da quelli deboli. Notiamo la differenza se ascoltiamo una nota a 10 metri o a 10 cm di distanza dalle corde di un piano oppure se battere il tasto con minore o maggiore forza. Se riportassimo nel nostro diagramma la stessa nota (La) ma con le 2 intensità sovrapposte otterremmo:

Il periodo (T), la frequenza (v) e la pulsazione (w) sono legate tra loro, cioè basta conoscere una di queste quantità per ottenere le altre due. L'ampiezza diversamente rimane indipendente:

Il Timbro e Fourier

Cos'è che distingue un La emesso da un flauto e un La emessa da un armonica a bocca? Due strumenti musicali possono avere la stessa frequenza e la stessa ampiezza ma ciò che distingue fondamentalmente un suono da un altro è il timbro ossia la diversa forma d'onda, la diversa variazione di pressione nel mezzo in cui si propaga; in altri termini in un diagramma pressione-tempo tali variazioni (in sec.), prodotte per esempio da un armonica a bocca, possono essere schematizzate così:

Quel che vediamo è un oscillazione periodica NON sinusoidale. Quest'ultimo termine lo ripeteremo spesso nel testo e ne daremo una definizione in notazione trigonometrica e successivamente in forma complessa.

Come potremo esprimere numericamente diversi timbri e in generale la forma di un'onda?

Con gli strumenti fin qui descritti possiamo solo quantificare la frequenza, l'ampiezza, ma non possiamo dire niente sulla forma d'onda, anche di natura elettromagneticha, se non con l'aiuto di Fourier.

© C o p y r i g h t     1 9 9 4 - 2 0 0 4 w w w . d i z i o n a r i o i n f o r m a t i c o . c o m