Il Dizionario Informatico, © www.dizionarioinformatico.com

Il Teorema di Fourier

"Qualunque segnale periodico può essere scomposto nella somma di un eventuale termine costante e di segni sinusoidali, dei quali il primo, avente lo stesso periodo e quindi la stessa frequenza del segnale considerato, si chiama prima armonica o fondamentale, e gli altri, aventi periodi sottomultipli e quindi frequenze multiple, si chiamano armoniche superiori"

In questo modo sembra possibile scomporre praticamente ogni moto o vibrazione periodica anche complessa in moti o vibrazioni più semplici basati su seni e coseni.

Prima di dare la definizione di armonica cominciamo a studiare le funzioni periodiche da cui derivano le armoniche, ossia le funzioni sinusoidali e cosinuisoidali.

ove A rimane l'ampiezza , w la pulsazione e la fase.

Sappiamo però che
ma ponendo
otteniamo a cos wx + b sen wx

Quindi con tale sostituzione siamo riusciti a riscrivere la nostra funzione in termini di seno e coseno, riassumendo:

Analogamente .
Quindi a e b sono le due nuove ampiezze e quel che è più interessante è l'assenza del coefficiente di fase nella nuova espressione;

Come abbiamo già visto la pulsazione w è 2/T, ma con il periodo T = 2 otteniamo che w=1 ossia abbiamo una singola pulsazione nell'intervallo 2. Se però cresce la frequenza di un onda cresce anche il numero di pulsazione poiché w = 2 v. Per fare un esempio supponiamo di avere una funzione in seno e coseno con w = 4 ossia
(fig 1):

Notiamo che nell'intervallo - + la somma di -sen4x e 5/2cos4x crea una nuova onda sinusoidale più amplifica e spostata in fase verso sinistra rispetto a 5/2cos4x. In realtà la fase nella funzione non è scomparsa ma è riscritta come somma di un opportuna funzione sinusoidale.

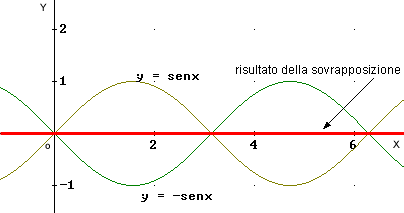
La somma di queste onde è un semplice esempio di quello che puo' accadere con le onde eletromagnetiche quando si verifica il fenomeno di interferenza: l'interferenza è quel che accade a due o più onde quando il risultato della loro sovrapposizione crea una nuova perturbazione periodica.

La nuova onda prodotta rimarrà sinusoidale se la sovrapposizione delle due onde generatrici manterrà la stessa pulsazione, anche se avranno fasi e ampiezze diverse. Nel caso però in cui due onde siano di medesima ampiezza ma sfasate l'una rispetto all'altra esattamente di 180°, ovvero quando il massimo di un onda coincide esattamente con il minimo dell'altra allora l'effetto della sovrapposizione delle onde è quello di annullarsi. (fig.2)

In questo caso diremo che le onde interferiscono in modo distruttivo.

Possiamo riportare un esempio pratico dell'effetto dell'interferenza con un esperimento condotto nel 1801 dal fisico inglese Thomas Young.

Dimostrò che in certe circostanze la luce non si comporta, come aveva dedotto Newton nel Seicento, come un flusso di particelle (concezione corpuscolare) bensì come un qualsiasi fenomeno ondulatorio.

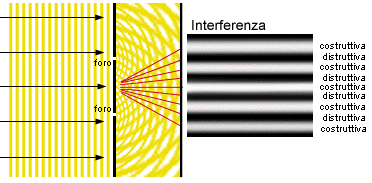
Infatti Young, facendo passare un fascio di luce bianca attraverso due fenditure molto strette su un diaframma in modo da creare l'effetto di diffrazione, osservò il fenomeno riportato in questa figura (fig. 3):

Le onde di luce emesse dai due fori si sovrappongono e dove le linee rosse evidenziano le zone costruttive l'effetto di questa interferenza si risolve proiettandosi in strisce sfumate di luce bianca, laddove le strisce rosse evidenziano zone di interferenza distruttiva le onde si annullano e si ha un effetto di oscurità (strisce nere).

Tornando alla fig. 1 invece, abbiamo fatto interferire tra loro due funzioni sinusoidali in modo costruttivo ossia abbiamo sovrapposto, in termini adottati in fisica, due treni d'onda con l'effetto di amplificare il segnale seppur leggermente.

Nel caso in cui vari la pulsazione come vedremo ora, la sovrapposizione produrrà un'onde non più sinusoidale periodica ma semplicemente un'onda periodica di periodo 2. Infatti a parità di intervallo la funzione seno ha il doppio delle pulsazioni rispetto alla funzione coseno. (fig.4)

Il Teorema di Fourier ci dice che è possibile scomporre un onda periodica come somma di funzioni sinusoidali più semplici, anche se spesso il calcolo fatto per ottenere tale scomposizione non è banale. Al contrario sommare onde sinusoidali è un operazione che sappiamo già fare.

In altri termini con opportune interferenze (somme) di onde più semplici si può ricostruire l'onda originale, in particolare un onda sonora oppure un segnale elettromagnetico. Eccone un esempio:

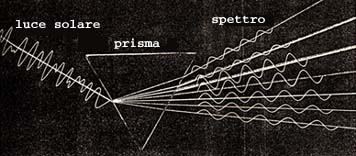
La luce

Ecco quel che succede se si scompone la luce in radiazioni di lunghezza d'onda diverse per mezzo di un prisma (dispersore).