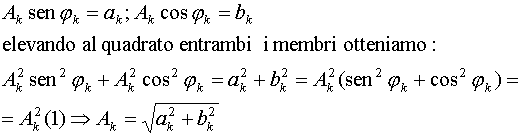La Serie di Fourier

Polinomi trigonometrici

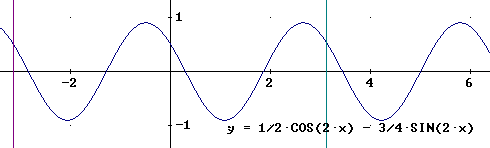
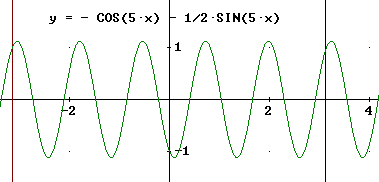
Le funzioni sinusoidali di periodo 2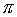 possono essere espresse nella forma:

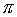
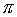
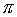
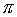
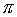
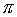
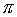
Ricordandoci che la pulsazione w = 2/T (misurata in radianti al secondo) e se la funzione sinuisoidale è di periodo minimo T = 2 abbiamo w = 2/2 = 1 cioè abbiamo un'oscillazione completa nell'intervallo 2 mentre se T = abbia esattamente 2 oscillazioni come si puo' vedere nella figura 5; nella figura 6 invece w = 2/T = 5.

fig.5

fig.6

In generale se la funzione ha come minimo periodo T=2/w, in un periodo 2 si compiono w oscillazioni complete. La prima espressione ha sì periodo minimo T = ma possiamo sempre considerarla come un espressione di periodo 2 giacchè compie in questo intervallo due oscillazioni esatte, questo vale anche per la seconda espressione e in generale per la seguente espressione:

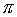
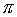
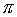
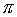
a ₁cosx+b₁senx+a₂cos2x+b₂sen2x+....+a_ncoskx+b_nsenkx.

Infatti anche la somma di piu' funzioni sinusoidali con pulsazioni diverse da ancora una funzione periodica di periodo 2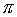, un esempio lo abbiamo visto in figura 4.
Non ci resta che riscrivere le somme delle funzioni sinuisoidali in forma compatta e aggiungere a ₀ /2.

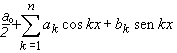
La costante a0

La costante a0>0 ha il semlice effetto di spostare l'onda prodotta dalla sommatoria verso l'alto oppure verso il basso se a<0 rispetto all'asse delle x. Nell'immagine consideriamo il contributo di una costante sommata a sen x.

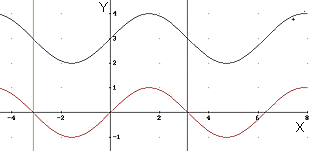fig.7	y = 3 + sen x
	y = sen x

Nel prossimo paragrafo, dedicato all'analisi armonica, questa costante ha valore nullo se il segnale e' alternato perchè tale costante rappresenta il valore medio della funzione periodica. Un esempio di segnale alternato, come vedremo è quello di un onda quadra.

Polinomio trigonometrico

fig.7a

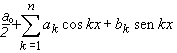prende il nome di Polinomio trigonometrico di ordine n.

Così ad esempio se abbiamo

i coefficienti sono a ₀=6, a₁=1, b₁=2, a₂=-3, b₂=1/3, a₃=0, b₃=-4.

Il problema dell'analisi armonica e' quello di sviluppare in serie trigonometrica, se e' possibile, la funzione f(x) di periodo 2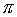 e quindi di calcolare il valore medio di f(x) e quello delle singole armoniche che compongono la funzione stessa.
Viceversa, affinchè la serie trigonometrica converga effettivamente a f(x) si deve rispettare

il Criterio (o Condizioni) di Dirichlet che impone:

1. f(x) deve essere definita nell'intervallo t₀-t₀+T; sono ammessi anche eventuali punti di discontinuità purchè in numero finito.
2. f(x) e la sua derivata primaf'(x) devono essere continue a tratti nell'intervallo t₀-t₀+T.

Se viene rispettata questa condizione possiamo scrivere che f(x) =  .
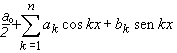Se f(x) soddisfa alle ipotesi del Teorema di Dirichlet parleremo di sviluppo di f(x) in serie di Fourier anche se la serie di Fourier di f(x) può non coincidere nei punti di discontinuità con f(x).

Le armoniche

Prima di vedere le formule per trovare i coefficienti della serie di Fourier diamo la definizione di armonica.

La funzione a ₁cosx+b₁senx viene detta prima armonica o armonica fondamentale della serie, o se valgono le condizioni di Dirichlet, della funzione f(x).
L'armonica fondamentale, come si puo' vedere nella fig. in basso, ha frequenza minima rispetto alle armoniche di ordine superiore ed è quella che da' il maggiore contributo nella costruzione dell'onda risultante della serie.
Chiamiamo invece la funzione a _kcosx+b_ksenx la k-esima armonica o armonica di ordine k della serie o, se vale il Criterio di Dirichlet, di f(x).

L'ampiezza della k-esima armonica
Riprendendo quanto detto precedentemente:

ma ponendo
otteniamo a cos wx + b sen wx.

L'ampiezza A _k della k-esima armonica possiamo trovarla con il seguente procedimento:

L'onda quadra

Un'onda quadra alternata di ampiezza Y= 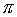/4 e periodo T si puo scrivere come:

fig.8

Se definiamo l'ampiezzaY=/4 otteniamo la seguente serie: sen x + (sen3x)/3 + (sen5x)/5 + ... in questo caso riprendendo la sommatoria in fig7a, a 0=a1=a2=...=0 (la funzione coseno scompare) mentre b1 = 1, b2 = 0, b3 = 1/3, b4 = 0, b5=1/5 ... In altri termini ak = 0, per ogni k, e bk = 0 se k e' pari e 1/k se k è dispari. L'onda è composta dalle armoniche di ordine dispari con ampiezza inversamente proporzionale alla frequenza e fase nulla. Le armoniche di ordine 3,5, 7 ecc. con ampiezze sempre meno significative, sommandosi a quella fondamentale, modellano e aggiustano le armoniche precedenti con il risultato di approssimarsi complesivamente all'onda quadra. Tale obbiettivo lo si può raggiungere anche sommando un numero finito e ridotto di armoniche poichè le armoniche di ordine n, all'aumentare di n, contano sempre meno. Nella sua formulazione matematica il teorema di Fourier ci permette di effettuare l'analisi armonica di un fenomeno periodico, ossia di determinare le ampiezze della frequenza fondamentale e delle armoniche di ordine superiore.

Lo spettrografo nella figura in basso misura le ampiezze delle armoniche ma si sarebbe potuto rappresentare anche un'altro spettro, quello delle fasi mediante segmenti proporzionali ai valori delle fasi delle varie armoniche.

Bastano infatti questi due spettri per poter risalire alla forma del segnale originale. La Trasformata di Fourier risulterà essere molto importante proprio perchè nel caso di una funzione discreta ci permette di ricavare l'elenco delle ampezze e delle fasi.

L'oscilloscopio invece ci mostra nel dominio del tempo la forma d'onda, ottenuta dalla somma delle prime due armoniche della serie.

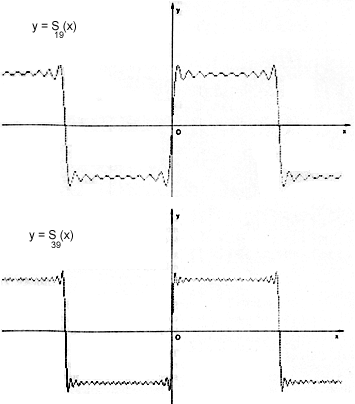
Non si può dire quante armoniche siano necessarie per definire un forma d'onda, ma il numero sarà tanto più elevato quanto più la forma dell'onda ha carattere impulsivo, proprio come l'onda quadra.

Se tracciamo il grafico sul piano cartesiano di y = S ₇(x) = sen x + (sen3x)/3 + (sen5x)/5 + (sen7x)/7 abbiamo la seguente approssimazione. In generale all'aumentare di n in S_n (x) otteniamo approssimazioni migliori, ma come si puo' notare, sarà sufficiente scegliere un n finito e nemmeno troppo grande per ricostruire l'onda quadra.

© C o p y r i g h t     1 9 9 4 - 2 0 0 4 w w w . d i z i o n a r i o i n f o r m a t i c o . c o m